How LLMs Sent Me Back to Logic and Linear Algebra
I went back to basics to rebuild my math foundation, and 50 days in, I've finally started in the right place.
Part of the From Logic to Transformers series
Table of Contents
50 days ago this equivalence made no sense to me. Today, I can explain it.
$$ \exists !xP(x) ↔︎ \exists x(P(x) \wedge \neg\exists y(P(y) \wedge y \neq x)) $$I went from “what the fck is this” to “ok, there is exactly one value of \(x\) such that \(P(x)\) is true”.
This is the first post in my learning journey series: From Logic to Transformers. I want to track my progress, so I can look back on how far I’ve come, and maybe help others on a similar path.
Why
I’ve been a software engineer for over a decade, mainly focused on backend systems. With all the recent AI developments, I became curious about Large Language Models (LLMs) and the hype around them. Naturally, I tried LLM-based tools in my pet projects and at work. My productivity went up. It felt like having a clever junior dev by my side, someone who can handle the heavy lifting but still needs guidance and direction.
The more I used these tools, the more I wanted to understand how and why they work under the hood. Understanding the why behind the tools has always led to deeper insights and helped me solve harder problems and design better systems.
But LLMs turned out to be a different beast. My attempts to understand them went nowhere. Books and blog posts only raised more questions. I even tried reading research papers, but the math did not click. Words like vector spaces and eigenvectors meant nothing to me. Matrix multiplications just worked in the code, but I had no idea why. I could follow the implementations line by line, but I could not see the reasoning behind them.
That frustration is what pushed me back to the basics.
Back to Basics
When I turned to math for Machine Learning (ML), most books started with vectors and matrices, then moved on to vector spaces and linear algebra. I had studied linear algebra back in university, but no one explained why things worked. Or maybe I just was not paying attention because I did not see how it connected to real-world problems.
I sometimes envy folks who went into game development. They realized early on that linear algebra was essential for graphics and physics, and they built solid foundations. I skipped that step, which is why the math felt like a wall when I hit it later.
Linear algebra starts simple, with vectors and their geometric meaning. But it gets steep quickly. The deeper you go, the more theorems and proofs you meet, each one building on top of the previous one. That is where I got stuck again: why do these proofs work, and how did the author come up with them?
That search for answers is what led me to the missing piece: logic.
Finding the Real Gap
At that point I realized something important: all proofs are built on logic. Every “therefore” in a textbook assumed a foundation I didn’t have. I had never studied logic formally, beyond a few AND/OR/NOT gates in a hardware course at university. No wonder proofs didn’t make sense.
So I decided to start from scratch. Learn logic, and re-learn linear algebra in parallel. One day logic, the next day linear algebra. Repeat until things start to click.
The Study Routine
I ended up with two books: How to Prove It (3rd edition) by Daniel J. Velleman and Introduction to Linear Algebra (2nd edition) by Serge Lang. I tried watching videos and courses, but they distracted me and I lost focus, so I narrowed down to just these two resources.

The process is simple. I read a chapter and work through the exercises that have answers to check myself. I also attempt others, using ChatGPT to verify or clarify when needed.
While reading, I take quick notes, highlighting anything that stands out or concepts I don’t know. After finishing a chapter, I read it again, review my notes, and turn them into Anki cards . On the second read I almost always catch things I missed, and my understanding gets deeper.
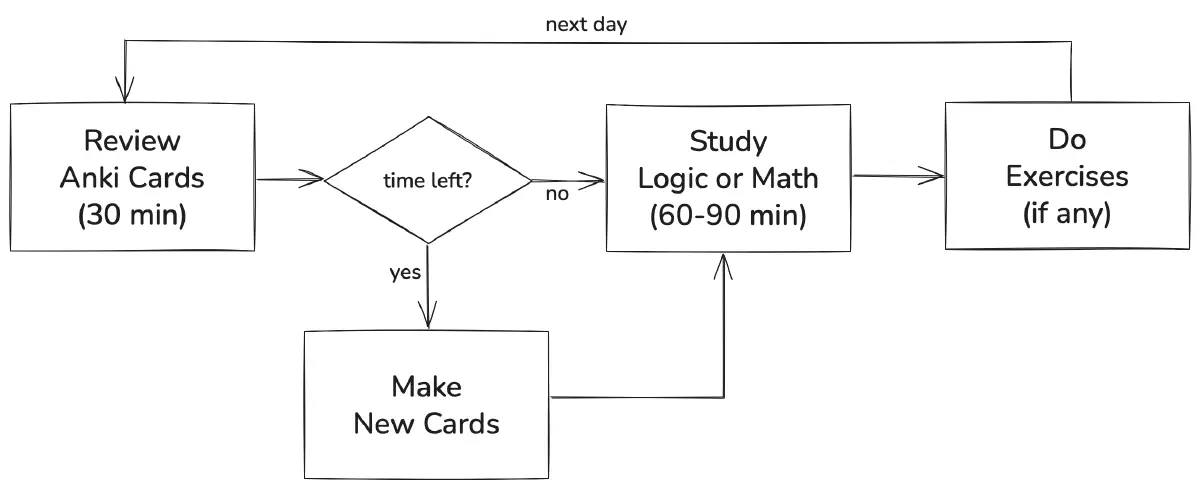
I study in the mornings, usually for 90 to 120 minutes, when my mind is fresh and math is a good fit for that time. The first 30 minutes go to Anki reviews from both decks, no matter if it is a logic or a math day. If the review is quick, I use the extra time to turn more notes into cards.
The next 60 to 90 minutes are for reading: logic one day, math the next. If a subsection ends with exercises, I solve them right away. At first, I could not solve many, and that was fine. Over time, as I built and reviewed more cards, problems that once seemed impossible started to feel manageable, and my intuition grew.
Progress After 50 Days
So, where am I after 50 days?
In logic, I have finished the Sentential and Quantificational logic chapters and I am now in the middle of Chapter 3 on Proofs. In linear algebra, I went through the chapters on Vectors, Matrices and Linear Equations, and Vector Spaces, and I am now in the middle of Chapter 4 on Linear Mappings.
Logic
The most memorable moment in logic was when I managed to derive \(A \backslash B = A\) from \(A \cap B = \emptyset\) and show they are equivalent.
Here is the full chain of reasoning (skip if you are not into the details):
- \(A \cap B = \emptyset\) is equivalent to \(\neg\exists x(x \in A \wedge x \in B)\) using the set definition
- which is equivalent to \(\forall x\neg(x \in A \wedge x \in B)\) using the quantifier negation law
- which is equivalent to \(\forall x(x \notin A ∨ x \notin B)\) using De Morgan’s law
- which is equivalent to \(\forall x(x \in A \rightarrow x \notin B)\) using the conditional law
- which is equivalent to \(\forall x((x \notin B \wedge x \in A) ↔︎ x \in A)\) using the biconditional law
- which is equivalent to \(\forall x(x \in A \backslash B ↔︎ x \in A)\) using the set definition
- which is equivalent to \(A \backslash B = A\).
Linear Algebra
The highlight of linear algebra was this exercise:
Let \(V\), \(W\) be two vector spaces and let \(F: V \rightarrow W\) be a linear map. Let \(U\) be the subset of \(V\) consisting of all elements \(v\) such that \(F(v) = O\). Prove that \(U\) is a subspace of \(V\).
Here is my scratch work. We need to prove 3 things:
- \(O \in U\)
- if \(v, w \in U\), then \(v + w \in U\)
- if \(v \in U\) and \(c\) is a scalar, then \(c * v \in U\)
Proof:
- Since \(F\) is linear, \(F(O) = O\). So \(O \in U\).
- Let \(v\) and \(w\) be arbitrary elements of \(U\). Using properties of linear map we have \(F(v + w) = F(v) + F(w) = O + O = O\). So \(v + w \in U\).
- Let \(v\) be an arbitrary element of \(U\) and \(c\) is a scalar. Using properties of linear map we have \(F(c * v) = c * F(v) = c * O = O\). So \(c * v \in U\).
- Therefore, \(U\) is a subspace of \(V\).
To my surprise, I knew exactly what to do and how to prove it. That was the best feeling in the world, and it motivates me to keep going.
Reflections So Far
At first, it felt like a rabbit hole. I did not understand my gaps or where to begin building the foundation. I jumped from LLM blog posts and papers to ML, then to linear algebra, and finally to logic. Now, 50 days in, I feel like I have finally found the right starting point.
The path has not been easy. Some days I spend an hour wrestling with a single logic problem. Other days I manage 6 pages of linear algebra in 2 hours. Progress is uneven, but consistency wins.
Right now, my pace is about 5–6 pages in 90 minutes. That may sound slow, but the goal is not speed. It is building understanding that lasts. Focusing on the process instead of the result makes the work sustainable and even enjoyable.
This journey from Logic to Transformers will take time, but the connections are already becoming clearer. Logic helps me understand the structure of arguments and follow proofs step by step. With that foundation, concepts in linear algebra that once felt like rules to memorize, such as why a set of vectors forms a subspace, now start to make sense. Little by little, the pieces are coming together, and I can see how each layer of understanding builds on top of the previous one.
What’s Next?
Over the next 50 days, the plan is to keep going with the books I am reading. I will probably finish linear algebra by then, but if not, that is fine. What matters is showing up every day and moving forward.
I will share updates along the way, including progress, lessons, and next steps. Maybe it will help someone else who feels lost in the why, like I was. I have found my starting point, and I hope you find yours too.
Sometimes the fastest way forward is realizing where you should have started all along. See you in the next post.